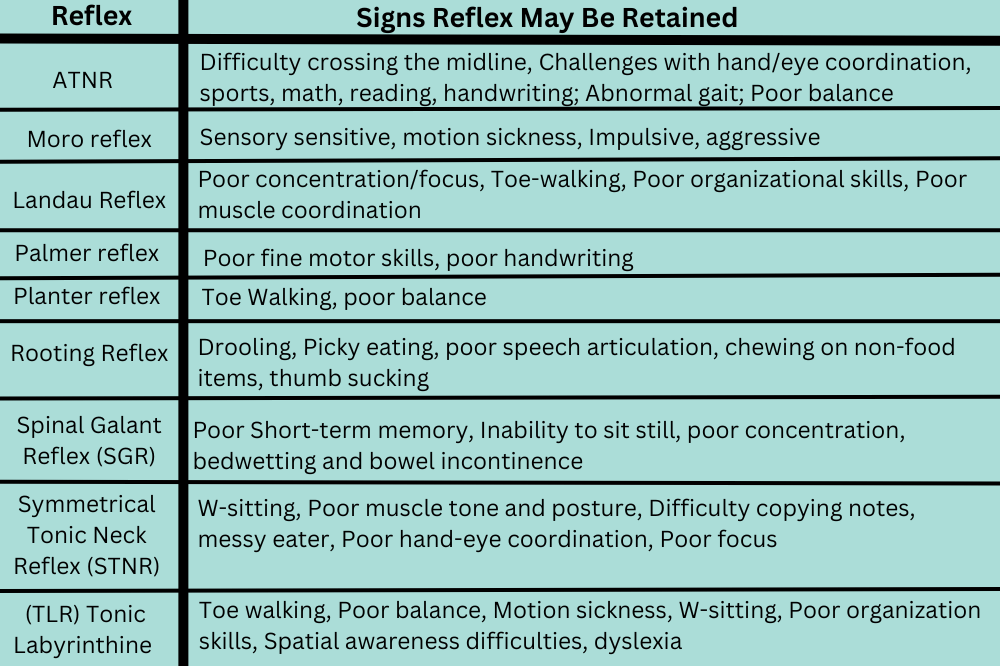
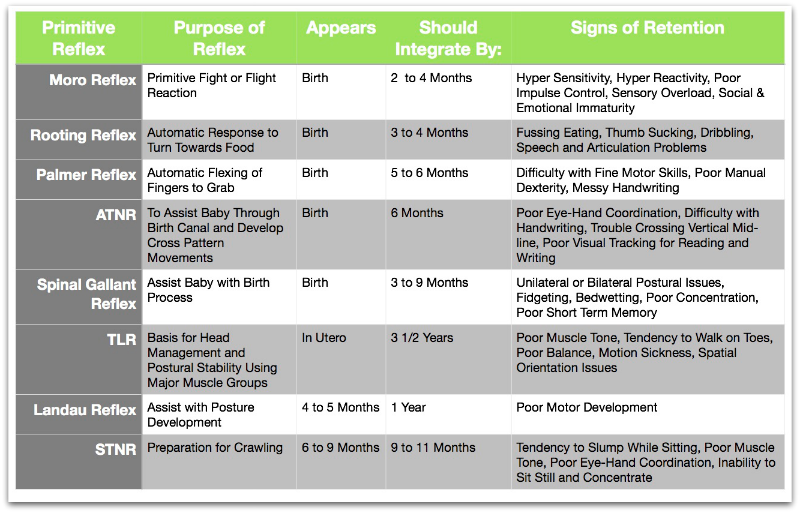
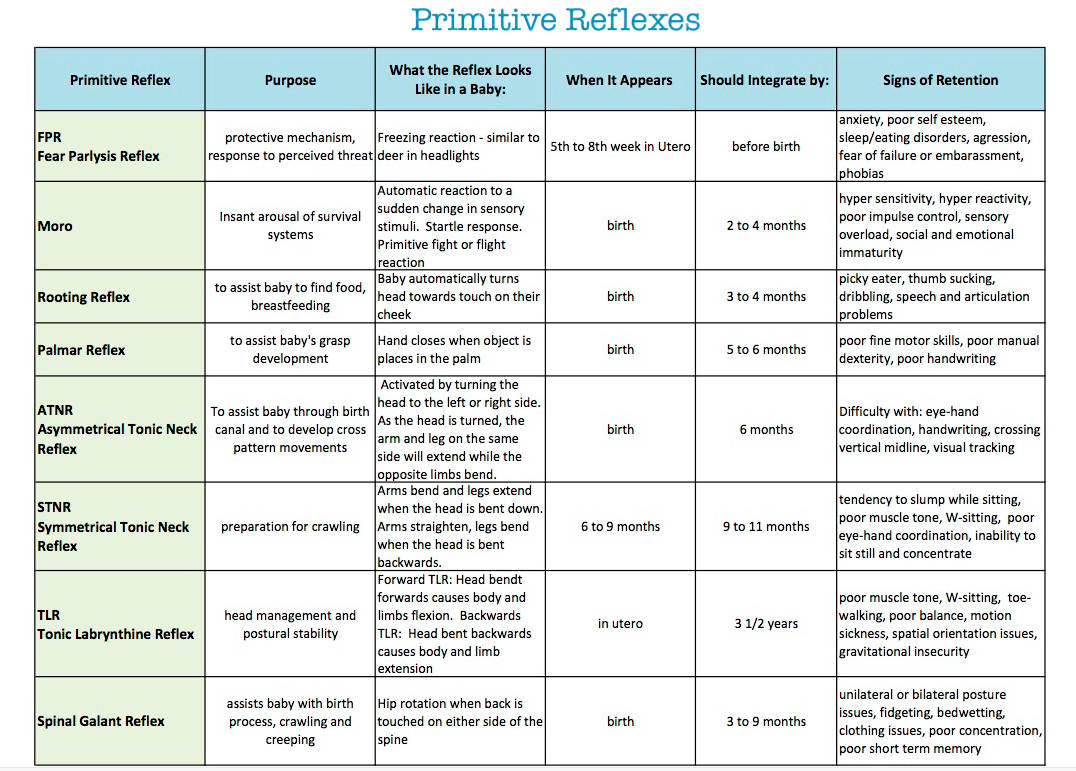
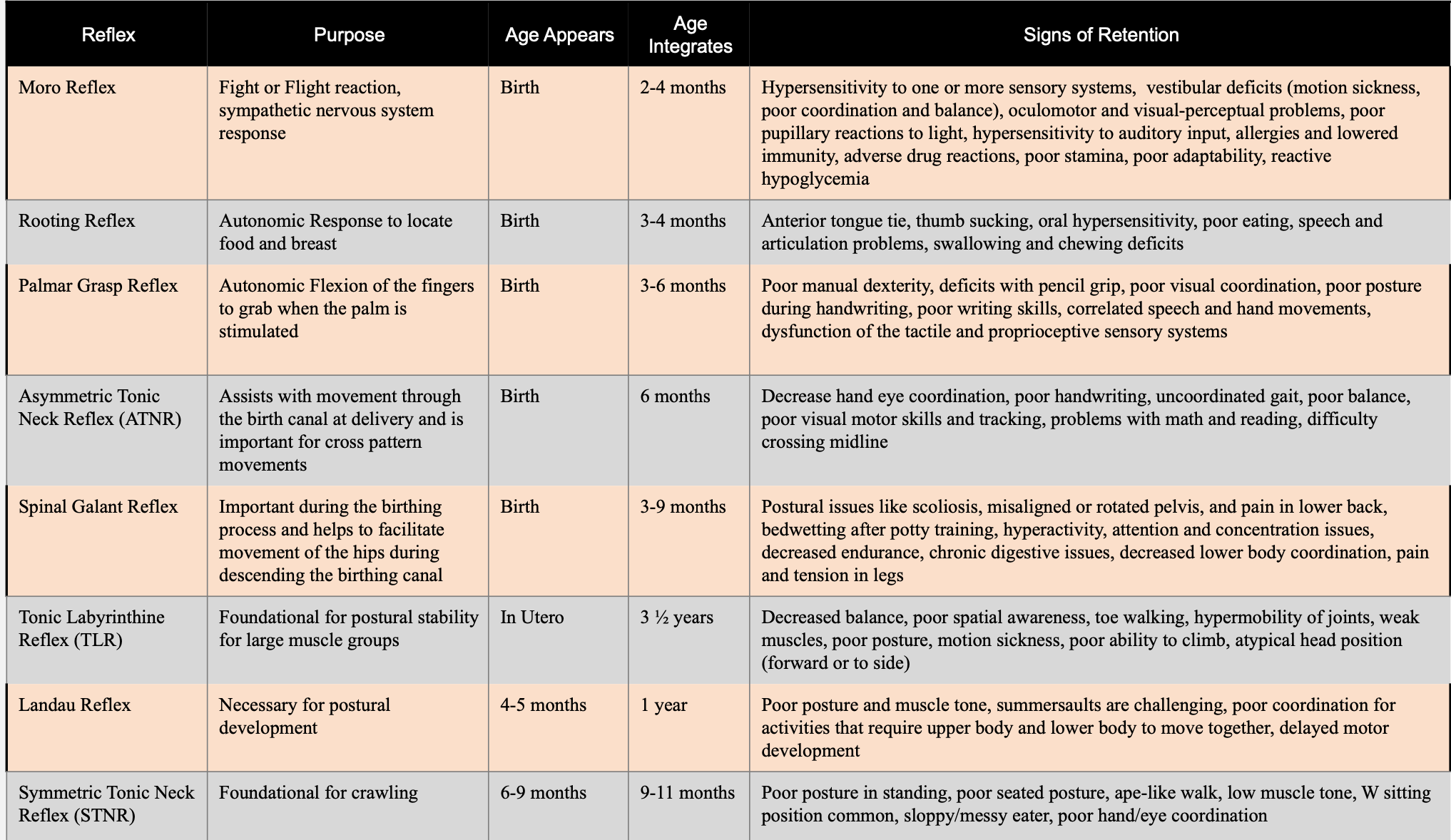
Primitive Reflex Chart
Primitive Reflex Chart - Find all the primitive roots of 13 13 my attempt: As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. A primitive root of a prime p p is an integer g g such that g (mod p) g (mod p) has. A primitive function of ex2 e x 2 ask question asked 11 years, 1 month ago modified 5 years, 6 months ago Answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. I was looking into some random number generation algorithms and 'primitive polynomial' came up a sufficient number of times that i decided to look into it in. In most natural examples i think. Since that 13 13 is a prime i need to look for g g such that g13−1 ≡ 1 (mod 13) g 13 1 ≡ 1 (mod 13) there are ϕ(12) = 4 ϕ (12) = 4. Primus, first), is what we might call an antiderivative or. 9 what is a primitive polynomial? Answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. Primus, first), is what we might call an antiderivative or. I'm trying to understand what primitive roots are for a given mod n mod n. Ask question asked 3 years, 3 months ago modified 3 years, 3 months ago In most natural examples i think. Wolfram's definition is as follows: Do holomorphic functions have primitive? Find all the primitive roots of 13 13 my attempt: I was looking into some random number generation algorithms and 'primitive polynomial' came up a sufficient number of times that i decided to look into it in. As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. I'm trying to understand what primitive roots are for a given mod n mod n. Wolfram's definition is as follows: As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. Do holomorphic functions have primitive? Since that 13 13 is a. Find all the primitive roots of 13 13 my attempt: As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. Do holomorphic functions have primitive? A primitive function of ex2 e x 2 ask question asked 11 years, 1 month ago. Answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. If u u and v v are relatively prime and of opposite parity, you do get a primitive triple, and you get all primitive triples in this. Ask question asked 3 years, 3 months ago modified 3 years, 3 months ago Primus, first), is what we might call an antiderivative or. I'm trying to understand what primitive roots are for a given mod n mod n. Find all the primitive roots of 13 13 my attempt: A primitive root of a prime p p is an integer. As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. I'm trying to understand what primitive roots are for a given mod n mod n. A primitive root of a prime p p is an integer g g such that g. Wolfram's definition is as follows: Find all the primitive roots of 13 13 my attempt: I'm trying to understand what primitive roots are for a given mod n mod n. Primus, first), is what we might call an antiderivative or. Answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that. Primus, first), is what we might call an antiderivative or. Since that 13 13 is a prime i need to look for g g such that g13−1 ≡ 1 (mod 13) g 13 1 ≡ 1 (mod 13) there are ϕ(12) = 4 ϕ (12) = 4. In most natural examples i think. Answers to the question of the integral. As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. Answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive. As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. Do holomorphic functions have primitive? A primitive function of ex2 e x 2 ask question asked 11 years, 1 month ago modified 5 years, 6 months ago Since that 13 13. Ask question asked 3 years, 3 months ago modified 3 years, 3 months ago A primitive function of ex2 e x 2 ask question asked 11 years, 1 month ago modified 5 years, 6 months ago In most natural examples i think. Primus, first), is what we might call an antiderivative or. A primitive root of a prime p p. I'm trying to understand what primitive roots are for a given mod n mod n. A primitive function of ex2 e x 2 ask question asked 11 years, 1 month ago modified 5 years, 6 months ago Wolfram's definition is as follows: Find all the primitive roots of 13 13 my attempt: Primus, first), is what we might call an antiderivative or. Since that 13 13 is a prime i need to look for g g such that g13−1 ≡ 1 (mod 13) g 13 1 ≡ 1 (mod 13) there are ϕ(12) = 4 ϕ (12) = 4. I was looking into some random number generation algorithms and 'primitive polynomial' came up a sufficient number of times that i decided to look into it in. As others have mentioned, we don't know efficient methods for finding generators for (z/pz)∗ (ℤ / p ℤ) ∗ without knowing the factorization of p − 1 p 1. Do holomorphic functions have primitive? If u u and v v are relatively prime and of opposite parity, you do get a primitive triple, and you get all primitive triples in this way. Answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. In most natural examples i think.What are Primitive Reflexes in 2020 Therapy infographic, Occupational therapy activities
What are Primitive Reflexes? Chicago Occupational Therapy Therapy infographic, Occupational
Primitive Reflex Integration Chart Ponasa
Parents and Carers Caring Hands Chiropractic
Primitive Reflex Integration The Autism Community in Action
Retained Primitive Reflexes as a Sign of Brain Imbalance
InspiralReflexChart Health care services, Reflexes, Primitive reflexes
Sprocket Therapy Primitive Reflexes Page Sprocket Therapy Solutions, LLC
Understanding Primitive Reflexes How They Impact Child Development and Intervention Strategies
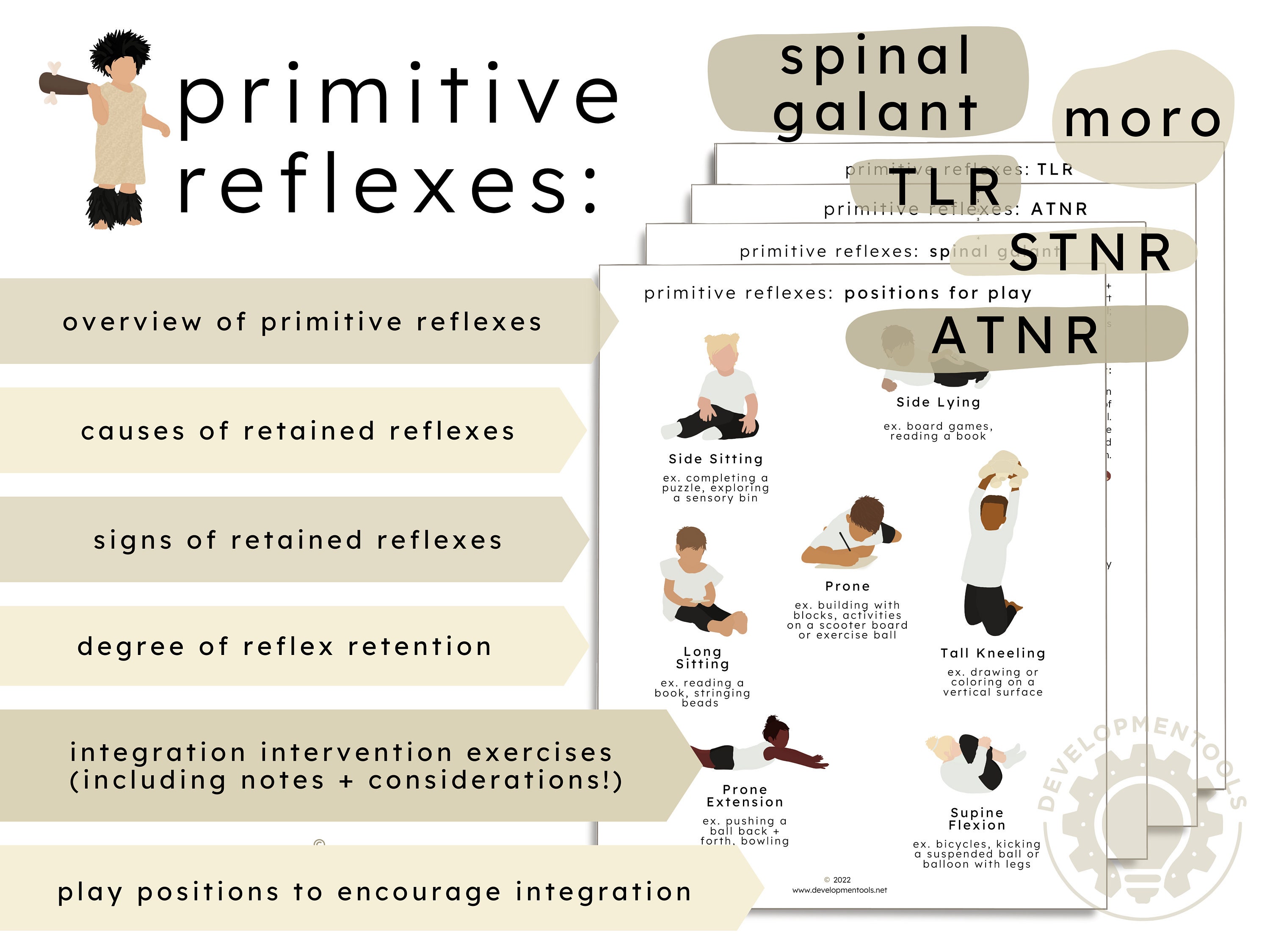
Instant Download Primitive Reflexes Integration, Exercises, Play Positions + Signs of
Ask Question Asked 3 Years, 3 Months Ago Modified 3 Years, 3 Months Ago
A Primitive Root Of A Prime P P Is An Integer G G Such That G (Mod P) G (Mod P) Has.
9 What Is A Primitive Polynomial?
Related Post: