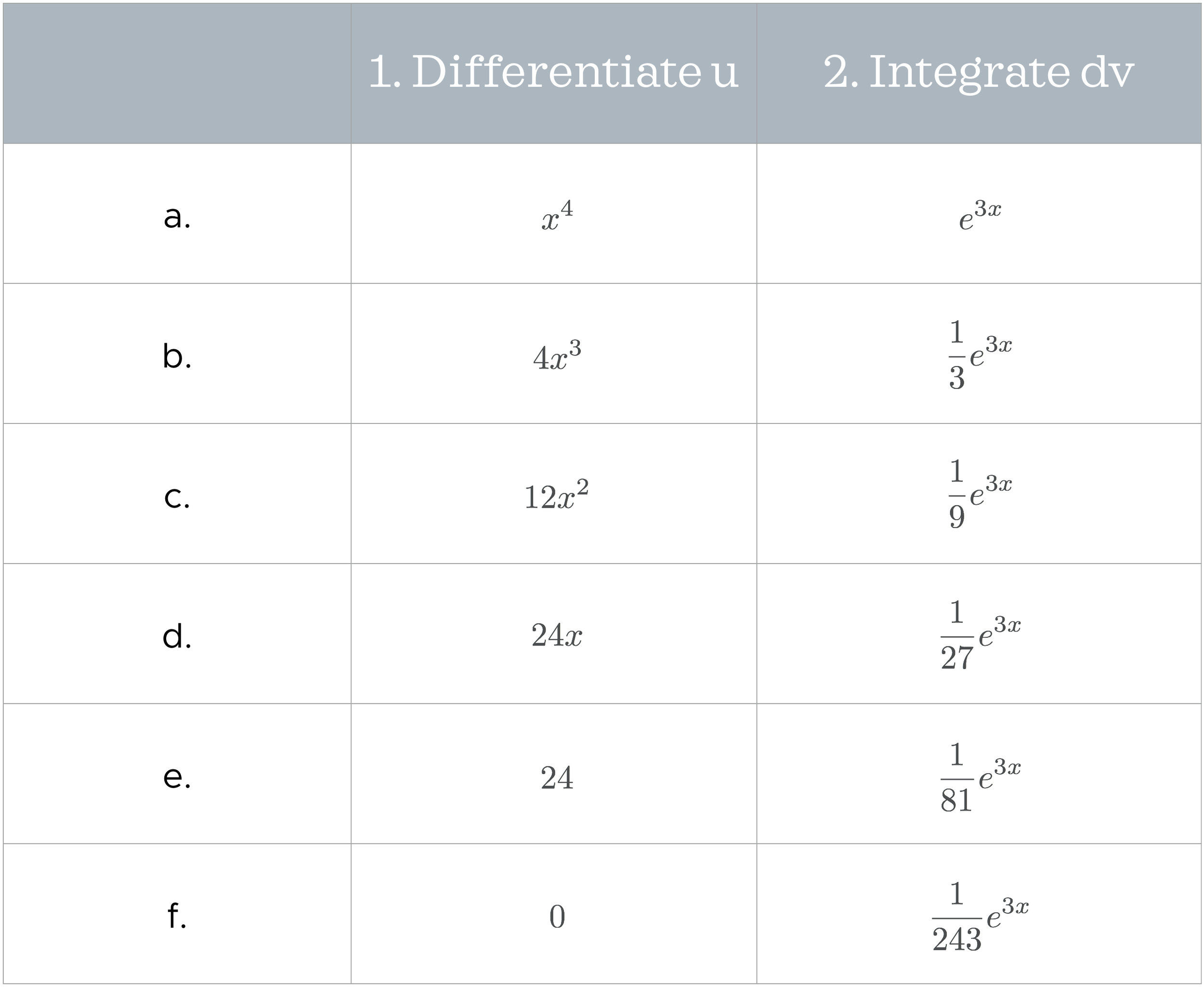
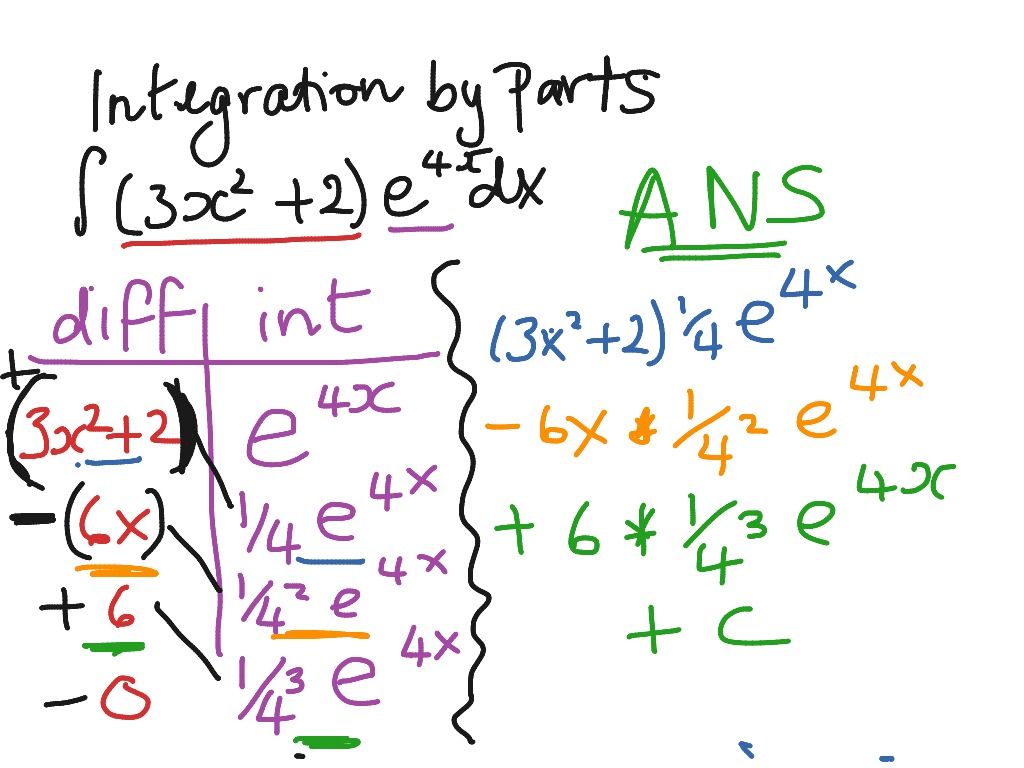Integration By Parts Chart

Integration By Parts Chart - But it is easiest to start. It is the inverse process of differentiation. Integration is finding the antiderivative of a function. Also double, triple and improper integrals. The fundamental theorem of calculus relates definite integration to differentiation and provides a method to compute the definite integral of a function when its antiderivative is known;. This can solve differential equations and evaluate definite integrals. From there, we develop the fundamental theorem of calculus, which relates. Integration is the union of elements to create a whole. Integration is the inverse of differentiation of algebraic and trigonometric expressions involving brackets and powers. Practice integration using trigonometric identities get 3 of 4 questions to level up!

All common integration techniques and even special functions are supported. The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating. Integration can be used to find areas, volumes, central points and many useful things. It is the inverse process of differentiation. Integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics. Integral calculus allows us to find a function whose differential is provided, so integrating is the inverse of differentiating. Learn about integration, its applications, and methods of integration using specific rules and. In this chapter, we first introduce the theory behind integration and use integrals to calculate areas. Integration is finding the antiderivative of a function. This can solve differential equations and evaluate definite integrals.

Integration By Parts Tabular Method YouTube

Free integral calculator helps you solve definite and indefinite integration problems. Integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics. Integral calculus allows us to find a function whose differential is provided, so integrating is the inverse of differentiating. Practice integration using trigonometric identities get 3 of 4 questions to.

Integration by parts tabular method Math, Calculus, Integrals ShowMe

But it is easiest to start. Integration is the union of elements to create a whole. Integration is finding the antiderivative of a function. Integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics. In this chapter, we first introduce the theory behind integration and use integrals to calculate areas.

core pure 3 notes integration by parts examples

The fundamental theorem of calculus relates definite integration to differentiation and provides a method to compute the definite integral of a function when its antiderivative is known;. The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating. All common integration techniques and even special functions are supported. This can solve differential equations and evaluate definite integrals. Integration.

Krista King Math Online math help Integration by Parts Everything You Need to Know

In calculus you will learn about differentiation, integration, circular. All common integration techniques and even special functions are supported. The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating. Integration is a way of adding slices to find the whole. Integration is the union of elements to create a whole.

Integration by parts (4 examples) Calculus YouTube

The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating. Also double, triple and improper integrals. Integral calculus allows us to find a function whose differential is provided, so integrating is the inverse of differentiating. Integration is finding the antiderivative of a function. This can solve differential equations and evaluate definite integrals.

Krista King Math Online math help Integration by Parts Everything You Need to Know

But it is easiest to start. This can solve differential equations and evaluate definite integrals. Integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics. The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating. Integration is finding the antiderivative of a function.

The Lansey Brothers' Blog Integration by Parts Miracle

Also double, triple and improper integrals. In this chapter, we first introduce the theory behind integration and use integrals to calculate areas. Integration is the union of elements to create a whole. From there, we develop the fundamental theorem of calculus, which relates. This can solve differential equations and evaluate definite integrals.

PPT Integration by parts PowerPoint Presentation, free download ID3317276

Integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics. Practice integration using trigonometric identities get 3 of 4 questions to level up! Integration can be used to find areas, volumes, central points and many useful things. This can solve differential equations and evaluate definite integrals. It is the inverse process.

Integration by Parts Example 4 YouTube

Integration is the union of elements to create a whole. Also double, triple and improper integrals. Practice integration using trigonometric identities get 3 of 4 questions to level up! Integral calculus allows us to find a function whose differential is provided, so integrating is the inverse of differentiating. Integration is finding the antiderivative of a function.

core pure 3 notes integration by parts examples

But it is easiest to start. This can solve differential equations and evaluate definite integrals. All common integration techniques and even special functions are supported. Integration is finding the antiderivative of a function. Integration is the inverse of differentiation of algebraic and trigonometric expressions involving brackets and powers.

Integration Is The Union Of Elements To Create A Whole.

This can solve differential equations and evaluate definite integrals. Integral calculus allows us to find a function whose differential is provided, so integrating is the inverse of differentiating. Learn about integration, its applications, and methods of integration using specific rules and. Integration can be used to find areas, volumes, central points and many useful things.

Also Double, Triple And Improper Integrals.

But it is easiest to start. In this chapter, we first introduce the theory behind integration and use integrals to calculate areas. The fundamental theorem of calculus relates definite integration to differentiation and provides a method to compute the definite integral of a function when its antiderivative is known;. Integration is a way of adding slices to find the whole.

Practice Integration Using Trigonometric Identities Get 3 Of 4 Questions To Level Up!

Integration is the inverse of differentiation of algebraic and trigonometric expressions involving brackets and powers. The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating. From there, we develop the fundamental theorem of calculus, which relates. Integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics.

It Is The Inverse Process Of Differentiation.

All common integration techniques and even special functions are supported. Free integral calculator helps you solve definite and indefinite integration problems. In calculus you will learn about differentiation, integration, circular. Integration is finding the antiderivative of a function.